Quantum Random Walk for Procedural Generation

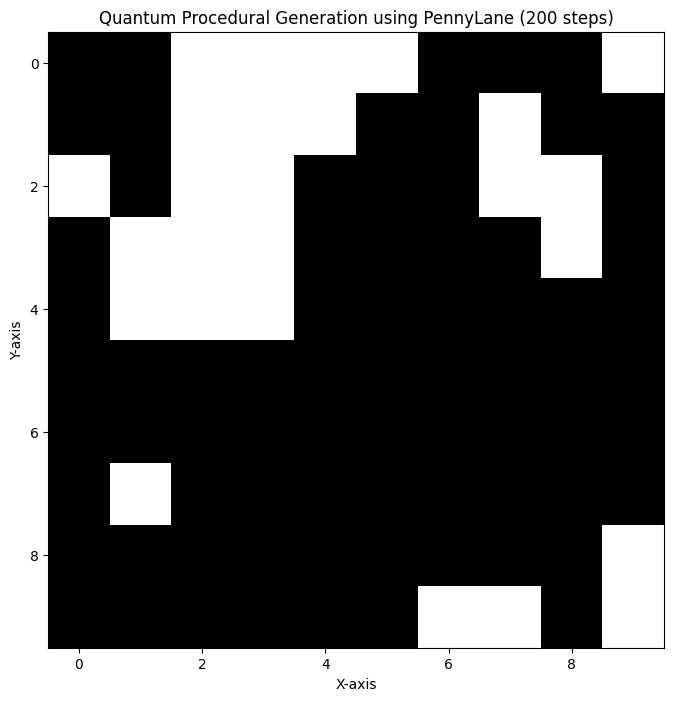
In this blog post, we’ll explore how quantum computing principles can be applied to procedural generation, specifically for generating random terrain. Procedural generation is essential in fields such as gaming, where vast landscapes and terrains need to be created with minimal human intervention. Here, we’ll use a quantum walk algorithm to generate random movements on a 2D grid, simulating terrain generation.

What is Quantum Procedural Generation (QPG)?

Quantum Procedural Generation leverages quantum mechanics to introduce randomness and superposition in procedural algorithms. Classical algorithms use pseudo-random number generators, but quantum computing offers a more intrinsic form of randomness through quantum states. This allows for innovative approaches in generating unpredictable terrain, patterns, or even paths within games.

In this example, we use a quantum walk to generate a random sequence of moves on a 2D grid.

Code Overview

We start by importing the necessary libraries. The code uses PennyLane, a quantum computing framework, along with NumPy and Matplotlib to handle the quantum operations and visualize the results.

import pennylane as qml
from pennylane import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display, clear_output

We are using 2 qubits to represent movement in two directions (X and Y) on a 2D grid. Each qubit will influence a specific movement direction based on the quantum states they take.

n_qubits = 2
dev = qml.device('default.qubit', wires=n_qubits, shots=2024)

Creating the Quantum Walk Function

The quantum_walk function defines how qubits will evolve to create random movements. We apply a Hadamard gate to each qubit, which puts them into a state of superposition—essentially allowing us to sample from a range of possibilities.

@qml.qnode(dev)
def quantum_walk():
    # Apply Hadamard gates to create superposition (randomness in movement)
    qml.Hadamard(wires=0)  # X-direction movement
    qml.Hadamard(wires=1)  # Y-direction movement
    return qml.sample(wires=[0, 1])

Setting Up the 2D Grid

We initialize a grid of size 10x10 and define the number of steps the quantum walker will take. Each step corresponds to a movement either up, down, left, or right. A dictionary is used to translate the quantum results into directional movements.

grid_size = 10
steps = 200

grid = np.zeros((grid_size, grid_size), dtype='int')
x, y = 0, 0

directions = {
    (0, 0): (0, 1),   # Move up
    (0, 1): (1, 0),   # Move right
    (1, 0): (0, -1),  # Move down
    (1, 1): (-1, 0)   # Move left
}

Running the Quantum Walk and Visualizing the Results

The loop below runs the quantum walk for a specified number of steps, updating the position on the grid based on the quantum result. Every few steps, the plot is updated to display the walker’s path on the grid. The movement is wrapped around the grid, ensuring that the walker doesn’t leave the boundary.

for step in range(steps):
    results = quantum_walk()  # Quantum walk result
    random_step = np.random.randint(len(results))  # Randomly select a step
    result = results[random_step]
    result_tuple = tuple(int(val) for val in result)  # Convert to tuple

    # Update the position based on movement direction
    dx, dy = directions[result_tuple]
    x, y = (x + dx) % grid_size, (y + dy) % grid_size
    grid[x, y] = 1

    if step % 1 == 0:
        ax.clear()
        ax.imshow(grid, cmap='Greys', interpolation='nearest')
        ax.set_xlabel('X-axis')
        ax.set_ylabel('Y-axis')
        ax.set_title(f"Quantum Procedural Generation using PennyLane ({step + 1} steps)")
        display(fig)
        clear_output(wait=True)
        plt.pause(0.1)

At the end of the loop, we display the final path generated by the quantum walk.

plt.show()

This code is just a basic implementation of Quantum Procedural Generation using random walk, where quantum computing principles are applied to randomly generate movements on a 2D grid by applying simple hadmard gates. The resulting patterns could be used for generating terrain in 2D games (like terraria) or simulating random exploration processes.

Full Notebook Download

You can access the full notebook using this link

Next Steps

There is currently active research on the use of QPG in games. Inspired by Dr. James R. Wotton, we’re currently researching the implementation of QPG for voxel based games like minecraft. This would be achived by generating a height map that would be then converted into the game terrarin using minetest, an open-source modding software for minecraft. Generating height maps can be done using various methods, each has its own limitations and advantages, none has been shown to be truly advantageous when compared to the classical methods for generating height maps (for example, using Perlin noise) yet.